En esta oportunidad quiero compartir mi experiencia trabajando en un proyecto que involucró la reconstrucción tridimensional de una escena en el entorno en Unibotics utilizando visión estéreo. Este proceso me permitió explorar y comprender la triangulación de las escenas a partir de dos imágenes capturadas desde diferentes ángulos. A continuación, te contaré cómo implementé el proceso y como logré obtener una representación visual precisa de los puntos en un espacio tridimensional utilizando herramientas como Python, OpenCV y las librerías GUI y HAL de Unibotics.
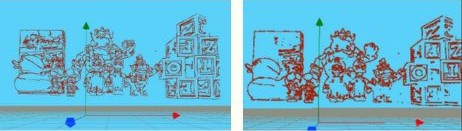
La imagen que se muestra acontinuación es la escena en Unibotics.

La imagen que se muestra acontinuación es la reconstrucción tridimensional de una escena en Unibotics.

Preparativos Iniciales:
Las posiciones tridimensionales de las cámaras respecto de la resferencia ROS se obtuvieron a través de HAL.getCameraPosition().
Procesamiento de Imágenes:
Una vez obtenidas las imágenes izquierda y derecha con la función HAL.getImage() de Unibotics, el siguiente paso fue preprocesar las imágenes para el análisis. En este caso, aumenté el brillo y contraste de las imágenes para mejorar su visualización y los resultados del proceso. Luego apliqué un filtro bilateral para suavizar y reducir el ruido, esto permitió mejorar la precisión de los bordes detectados.
A continuación se presentan a la izquierda las imágenes obtenidas con la función de Unibotics y la imagen preprocesada con aumento de contraste y brillo a su derecha.

Izquierda: imagen sin preprocesar, Derecha: imagen preprocesada.
El filtro bilateral se puede setear, cuando se aumentan los valores del filtro se obtienen menos puntos y cuando se disminuye la accion del filtro se obtienen más puntos.

Izquierda: mayor filtro, menos puntos. Derecha: menor filtro, más puntos.
Detección de Bordes y Coincidencias:
Con las imágenes preprocesadas, pasé al siguiente paso: la detección de bordes. Utilicé el detector de bordes de Canny para identificar las áreas de alto contraste en ambas imágenes. Esto permitió crear una representación gráfica de los contornos. Luego se extraen las coordenadas de los puntos de estos detalles y contornos con la función cv2.findContours. Con estos puntos detectados ya podemos encontrar las coincidencias entre ambas imágenes.
Se muestra a continuación la busqueda de coincidencias entre la imagen izquierda y la imagen derecha.
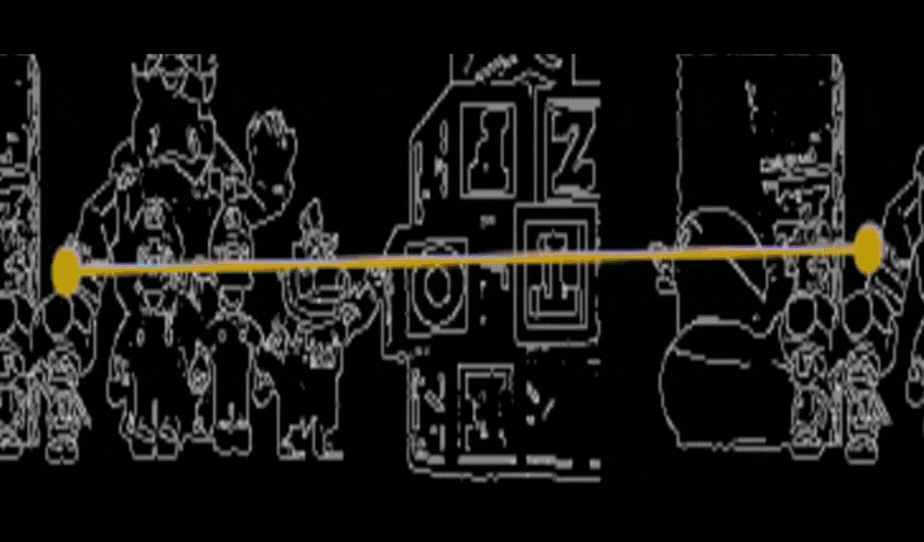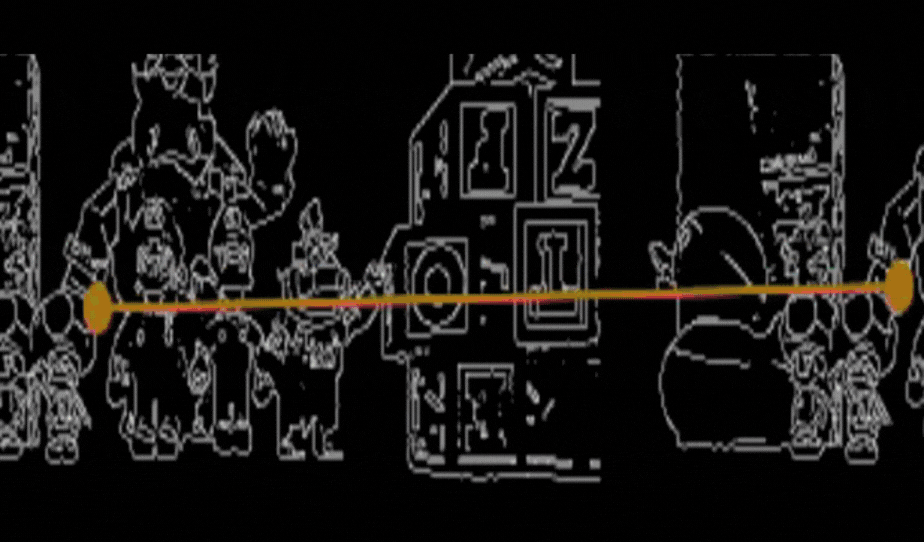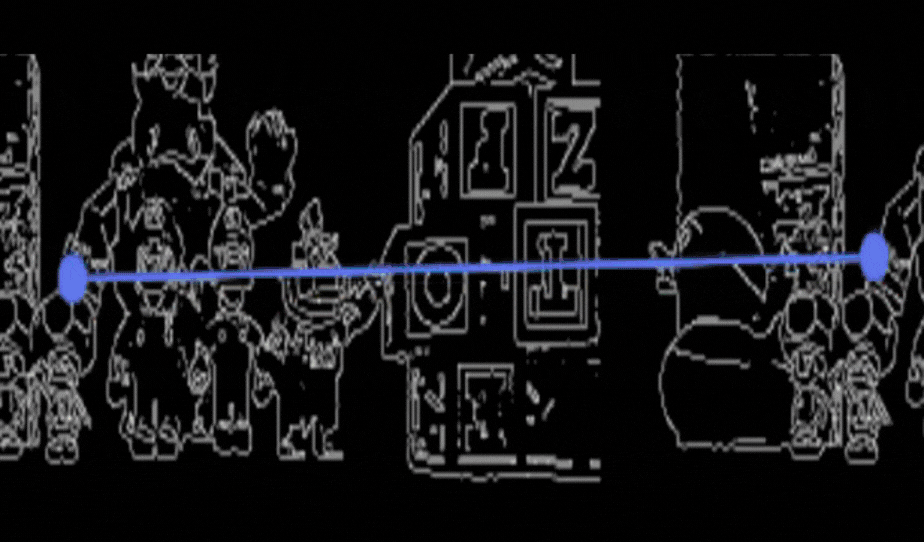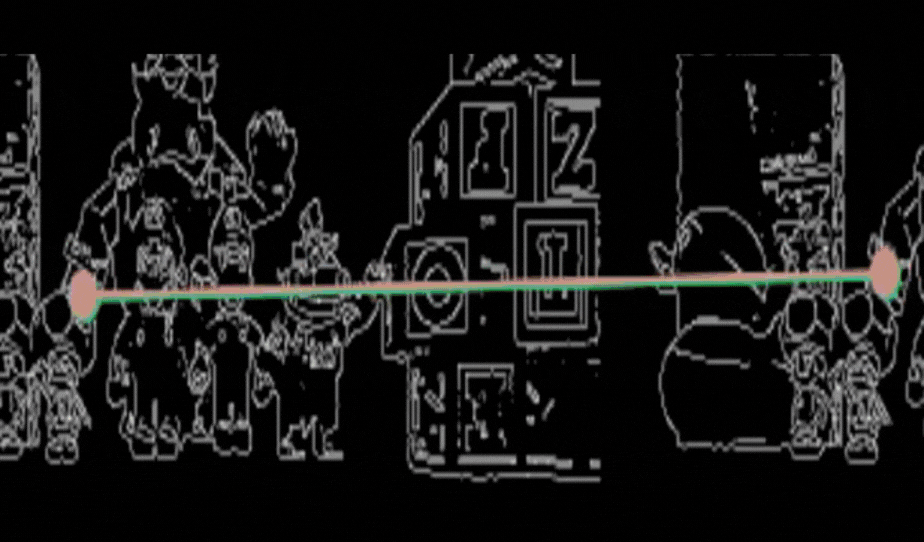
Apliqué la técnica de “matchTemplate” de OpenCV. Aquí, seleccioné una pequeña región de la imagen izquierda, alrededor de cada punto de los bordes, y busqué su correspondencia en la imagen derecha. Se muestran los resultados de esas coincidencias con la siguiente función GUI.showImages(img_left,img_right,True).
Cálculo de la Profundidad y Triangulación:
Utilizando los puntos correspondientes detectados en las imágenes izquierda y derecha, calculé la disparidad entre ellos. La disparidad es la diferencia en la posición horizontal de un punto entre las dos imágenes, y a partir de ella pude calcular la profundidad del punto en 3D.
Luego, utilicé las coordenadas de los puntos claves en la imagen izquierda (x_L , y_L) y la profundidad (Z) para calcular las coordenadas tridimensionales del punto en el espacio. Dos puntos en el espacio definen una recta, hacemos esto en la imagen izquierda y en la imagen derecha. Imaginemos dos rectas en el espacio que se cruzan pero no se cortan cómo dos avenidas que se cruzan en un puente. La mínima distancia entre esas rectas, avenidas en nuestro ejemplo, sería la altura del puente. Geométricamente hallamos un punto en la avenida sobre el puente y un punto en la avenida bajo el puente. El punto tridimensional que vamos a plotear es el punto medio de ellos.
Es importante mencionar que esto se denomina triangulación canónica, no se usaron funciones establecidas como “cv2.triangulatePoints()”.
Visualización en 3D:
Finalmente, todos los puntos 3D calculados fueron representados en el espacio tridimensional con GUI.ShowNewPoints(points_3D) utilizando la interfaz gráfica de Unibotics, donde cada punto se mostró con un color rojizo, permitiendo observar su distribución espacial.
Estas coordenadas en 3D fueron luego escaladas y ajustadas con un desplazamiento para adaptarlas a un sistema de visualización más adecuado.

Como no se distinguen bien los puntos estando todos de un solo color, después de obtener las coordenadas de X e Y de la imagen izquierda, he obtenido el valor del pixel de cada posición. Luego, esos valores los almaceno en las variables R, G, B respectivamente, para luego poder pasarlo al parámetro de visualización.

Al ajustar el umbral de “canny” se pueden obtener más o menos detalles en el resultado final, teniendo en cuenta que a más puntos, más tiempo de ejecución. Obteniendo tiempos de ejecución desde 3min hasta 15min apróximadamente.

También he probado procesar las imágenes sin aplicar un filtro bilateral, el resultado que se visualiza es que al no haber un filtrado hay más puntos y el resultado visual de la reconstrucción 3D se vé más completo. Sin embargo el tiempo de las detecciones de coincidencias e impresión de los puntos aumenta de 15min a 20min aproximadamente.






