Imagina un robot que se orienta en su entorno igual que tú reconoces puntos de referencia al caminar por una ciudad desconocida. Ese el el objetivo de la práctica Marker Based Visual Loc en Unibotics.

Mi enfoque ha sido demostrar cómo, con una imagen, algunos marcadores y un pequeño cálculo, se puede obtener una estimación precisa de la pose del robot (posición + orientación).
En esta entrada recorreré cada fase del pipeline — desde la calibración de la cámara y la detección de AprilTags hasta la estimación de pose y la proyección de coordenadas al mapa global — pero con un giro retador: he optado por prescindir de las multiplicaciones matriciales tradicionales para aligerar el código y reducir el coste computacional. El resultado es un ejemplo compacto pero completo de localización visual.
1. Preparación del entorno
Primero he cargado todas las librerías necesarias como pyapriltags y definido los parámetros de la cámara (matriz intrínseca y coeficientes de distorsión). Siguiendo la recomendacion.
2. Lectura de AprilTags
En esta fase seguí las indicaciones de la documentación y se ha cargado un archivo YAML que contiene la posición y orientación de cada AprilTag en el entorno simulado.
3. Bucle principal
Todo lo que ocurre a continuación está dentro de un while True, el corazón de la práctica.
Se obtuvo un fotograma con HAL.getImage() y se convirtió a escala de grises: esto hace que el detector trabaje más rápido y con menos ruido.
Luego se pasó la imagen al detector. Si se detecta al menos un marcador, marcamos sus cuatro esquinas y su centro en pantalla. Y además se decodifica para extraer sus coordenadas 3D.
Con las esquinas 2D (image_points) y las coordenadas 3D modeladas del tag (object_points), se resolvió solvePnP. El par (rvec, tvec) entregó eje-angulo de rotación y traslación cámara → tag.
Cada familia de tags está colocada con orientaciones distintas. En este paso se realizó un cálculo y un pos-proceso condicional para reordenar los ejes de tvec y así llevarlos al mismo sistema de referencia global.
Aquí viene la parte interesante, en lugar de recurrir a cadenas de matrices, decidí calcular el yaw con un ingenioso “duelo de tangentes”. Primero medí cuánto se desvía el centro del AprilTag respecto al punto principal de la cámara, lo que entregó el ángulo puramente visual que ve la lente. Luego obtuve, a partir de la traslación calculada por solvePnP, el ángulo real que separa la cámara del tag en el espacio. Al restar esas dos perspectivas con una sencilla identidad trigonométrica —tan(θ − α)— pude extraer la orientación horizontal del robot. El resultado es un cálculo ligero que actúa como brújula visual en tiempo real, sin multiplicaciones de matrices ni esfuerzos extra.
De aquí en adelante se llamó a GUI.showEstimatedPose(x, y, yaw) para pintar en la interfaz. En paralelo se envió al robot comandos simples: velocidad lineal y angular respectivamente(HAL.setV, HAL.setW). Para una navegación de demostración.
Estos son los resultados:
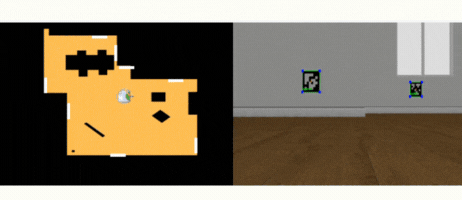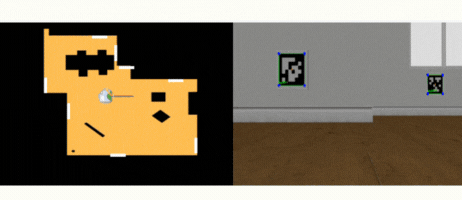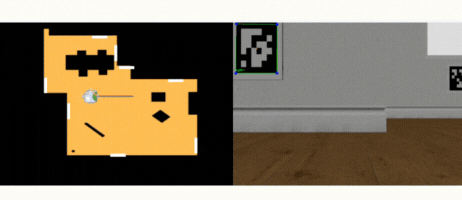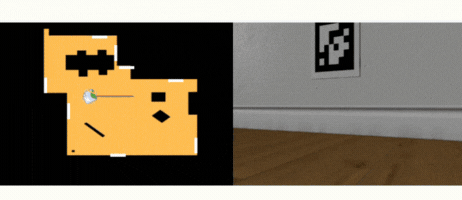
Por último se ha añadido un condicional de que si no se detecta ningún tag entonces se apoye en la odometría (HAL.getOdom()) y realice un giro hasta encontrar el siguiente Tag.
Uno de los retos de la práctica aparece cuando el robot se enfrenta a AprilTags lejanos —más de cuatro metros— o vistos con ángulos muy oblicuos. A esas distancias el ruido óptico se amplifica y complica la geometría. En la detección del Tag 4, qué se encuentra a más de 4 metros y en ángulo mayor a 45°, el eje ángulo que entrega o simula, es un eje ángulo qué falla en su coordenada X, parece una simulación seteada así. Lo que hace simplemente a usar odometría cuando el ángulo de visión del Tag es menor de 45° o a distancias menor a 4 metros. Sigo afinando esta fase.
Dejo una muestra visual en el siguiente vídeo, a pesar que hay problemas con la visualización de los gráficos en Unibotics. La línea azul representa el recorrido real del robot. Y la línea roja el recorrido de la estimación calculada.





